A Toy Calculator#
About Project 3#
Project 3 is a team project. You have already been divided into several pgroups. You should start p3 as soon as possible. To start your p3, here is what you should do:
Setup Drone. Only one person in a group needs to setup Drone. The process is similar to p2. Make sure you check the “Allow Pull Requests” when creating secret.
Connect to the non private p3 channel on MM and introduce yourself*
Each student carefully read p3 description and ensures they fully understand it*
Before starting to code each member draws hierarchy diagrams (as we saw in the lectures)
All team members meet (online or offline) to discuss their understanding of p3 and compare their diagrams
Argue on which diagram seems the most appropriate and will lead to the nicest coding experience
Once a best diagram is agreed upon, share the work fairly among all students
Students with much expertise must help the beginners
Beginners must ensure they understand what more advanced students are doing
P3 grade will be based on the final submission, a self evaluation survey, git commits, help provided to or asked by beginners
for future discussions you can use your private channel, but we want to ensure all students are present and ready to work
Stack-based Calculator#
Before we start doing a “real” calculator, let’s learn how to implement a calculator by using stack. A stack is a data structure that allows you to push and pop elements. It is a LIFO (Last In First Out) data structure. For example, if you push 1, 2, 3, 4, 5 to the stack, you will get 5, 4, 3, 2, 1 when you pop them out.
Stack vs Queue#
How do we implement a stack in C++?
C++ has a strong library called STL (Standard Template Library). It is composed of:
Containers
Iterators
Algorithms
Functions
STL Containers provide us with several handy and efficient implementation of data structures. For example, we can use std::stack to implement a stack. Here is how we can use std::stack:
#include <stack>
#include <iostream>
int main() {
std::stack<int> s;
s.push(1);
s.push(2);
s.push(3);
s.push(4);
s.push(5);
while (!s.empty()) {
std::cout << s.top() << std::endl;
s.pop();
}
}
Tip
You need to include <stack> to use std::stack.
The output of the above program is:
5
4
3
2
1
Besides std::stack, STL also provides std::queue, std::set, std::map and std::vector which are commonly used. You can read more about them in the STL Reference.
Now let’s implement a stack-based calculator.
This calculator is quite simple and limited. It only supports the following operations:
+: addition-: subtraction*: multiplication/: division
To simplify the process, the number can only be 1 digit, and no space is allowed between the number and the operator. For example, 1+2 is valid, but 1 + 2 is not. The calculator will read the input from the standard input (i.e. keyboard) and output the result to the standard output (i.e. screen). And no parentheses are allowed.
Before we start writing the code, let’s first understand how the algorithm works.
Simplified version of Shunting Yard Algorithm#
Before we introduce this quite compilcated algorithm, let’s first understand the concept of infix expression and postfix expression. An infix expression is an expression that contains operators and operands. For example, 1 + 2 is an infix expression. An postfix expression is an expression that contains operators and operands, but the operators are written after the operands. For example, 1 2 + is a postfix expression. We also assume that the operators can only be one of +-*/ (they are all left-associative). The following table shows the conversion between infix expression and postfix expression:
Infix Expression |
Postfix Expression |
|---|---|
|
|
|
|
|
|
|
|
The algorithm is called Shunting Yard Algorithm (invented by Edsger Dijkstra). It is a stack-based algorithm that converts an infix expression to a postfix expression. The algorithm is quite complicated and long (and is not quite generally and commonly used). We will only use a simplified version of it.
But why do wee need to do the conversion? Why is postfix expression better than infix expression? The answer is that postfix expression is easier to evaluate. For example, to evaluate 1 + 2 * 3, we can first convert it to 1 2 3 * +. Then we can evaluate it by using a stack. (Do some demonstration here to show that it is easier to evaluate a postfix expression.)
The simplified version of the Shunting Yard Algorithm is as follows:

Shunting Yard Algorithm Demo#
while there are tokens to be read:
read a token
if the token is:
- a number:
put it into the output queue
- an operator o1:
while (there is an operator o2 at the top of the operator stack, and
(o2 has greater precedence than o1 or they have the same precedence)):
pop o2 from the operator stack into the output queue
push o1 onto the operator stack
/* After the while loop, pop the remaining items from the operator stack into the output queue. */
while there are tokens on the operator stack:
pop the operator from the operator stack onto the output queue
(Modified from Wikipedia)
Suffix Expression evaluation#
Now we know how to convert an infix expression to a postfix expression. But how do we evaluate a postfix expression? The answer is that we can use a stack to do it. The algorithm is as follows:
Create a stack to store numbers.
Scan the output queue (which we generated from the last step) from left to right and do the following for every scanned element
If the element is a number, push it into the stack
If the element is an operator, pop it from the queue. Evaluate the operator and push the result back to the stack
When the expression is ended, the number in the stack is the final answer
Several containers and functions might be useful to implement this calculator:
std::stackstd::queuestd::stringstd::getlinestd::isdigit
Reference Code#
#include <iostream>
#include <queue>
#include <stack>
#include <string>
#include <string_view>
bool is_greater(char a, char b) {
// Judge the priority of the two operators
// Return true if a is greater thean b
if (a == '*' || a == '/') {
if (b == '+' || b == '-') {
return true;
}
return false;
} else {
return false;
}
}
bool is_greater_or_equal(char a, char b) {
// Judge the priority of the two operators
// Return true if a is greater or equal than b
return !(is_greater(b, a));
}
void move_op(char op1, std::queue<char> &output, std::stack<char> &ops) {
// op1 is the incoming operator
while (!ops.empty() && is_greater_or_equal(ops.top(), op1)) {
output.push(ops.top());
ops.pop();
}
}
void get_suffix(std::string_view input, std::queue<char> &output) {
std::stack<char> ops;
for (auto &c : input) {
// Iterate the string
// std::cout << c;
if (std::isdigit(c)) {
output.push(c);
} else {
if (ops.empty()) {
ops.push(c);
} else {
move_op(c, output, ops);
ops.push(c);
}
}
}
while (!ops.empty()) {
output.push(ops.top());
ops.pop();
}
}
void print_queue(std::queue<char> q) {
// Make a copy of the queue
std::cout << "The suffix expression is: ";
while (!q.empty()) {
std::cout << q.front();
q.pop();
}
std::cout << "\n";
}
float evaluate_suffix(std::queue<char> &suffix) {
std::stack<float> nums;
while (!suffix.empty()) {
if (std::isdigit(suffix.front())) {
nums.push(suffix.front() - '0');
} else {
float a = nums.top();
nums.pop();
float b = nums.top();
nums.pop();
switch (suffix.front()) {
case '+':
nums.push(a + b);
break;
case '-':
nums.push(b - a);
break;
case '*':
nums.push(a * b);
break;
case '/':
nums.push(b / a);
break;
}
}
suffix.pop();
}
return nums.top();
}
int main() {
std::queue<char> output;
std::string input;
std::getline(std::cin, input);
get_suffix(input, output);
print_queue(output);
std::cout << "The result is: " << evaluate_suffix(output) << "\n";
}
Advanced Calculator#
(Introduce some interesting and basic concepts that you may learn in future courses)
In the previous section, we have implemented a simple calculator. But there are some problems:
Not support negative, real numbers
Not support left and right parentheses
Not support space (fix available)
Hard to generalize
Why is it hard to generalize? Because the Grunting Yard Algorithm is not a general algorithm. For example, if we want to implement a calculator that support functions like sin, cos, tan, log, ln, sqrt, etc., we can not use the Grunting Yard Algorithm directly. Moreover, compicated symbols like ^ and ! are not supported by the Grunting Yard Algorithm either.
In modern programming languages, the Grunting Yard Algorithm is not used to implement a calculator. Instead, a lexer and a parser is used. The lexer is used to split the input string into tokens, and the parser is used to parse the tokens into an abstract syntax tree (AST). The AST is then evaluated to get the result.
There are some programs like flex and bison that can generate a lexer and a parser automatically.
A Toy Calculator Generated by flex and bison#
(Source code based on this Github Repo)
Copy the following code to calc.y:
%{
#include <iostream>
#include <cmath>
#include "mem.h"
extern std::map<std::string, double> variable_map;
extern unsigned int var_counter;
int yylex(void);
void yyerror(char *);
%}
%union{
char index[100];
double num;
}
%token<num> T_FLOAT T_INT
%token<num> OP_POW OP_DIV OP_MUL OP_ADD OP_SUB OP_EQL
%token<num> EOL
%token<num> SYM_PRNL SYM_PRNR
%token<num> FUNC_SIN FUNC_COS
%token<num> CMD_EXT
%token<index> T_IDEN
%type<num> strt
%type<num> stmt
%type<num> expr
%type<num> term
%type<num> unary
%type<num> pow
%type<num> factor
%right OP_EQL
%left OP_ADD OP_SUB
%left OP_MUL OP_DIV
%left OP_POW
%%
strt: strt stmt EOL { std::cout << $2 << "\n"; }
| strt EOL { std::cout << "\n"; }
| strt CMD_EXT { std::cout << ">> Bye!\n"; exit(0); }
| {}
;
stmt: T_IDEN OP_EQL expr { $$ = $3; set_variable($1, $3);}
| expr { $$ = $1; }
;
expr: expr OP_ADD term { $$ = $1 + $3; }
| expr OP_SUB term { $$ = $1 - $3; }
| term { $$ = $1; }
;
term: term OP_MUL unary { $$ = $1 * $3; }
| term OP_DIV unary { $$ = $1 / $3; }
| unary { $$ = $1; }
;
unary: OP_SUB unary { $$ = $2 * -1; }
| pow { $$ = $1; }
;
pow: factor OP_POW pow { $$ = std::pow($1,$3); }
| factor { $$ = $1; }
;
factor: T_IDEN { $$ = get_variable($1); }
| T_INT { $$ = $1; }
| T_FLOAT { $$ = $1; }
| SYM_PRNL expr SYM_PRNR { $$ = ($2); }
| FUNC_SIN SYM_PRNL expr SYM_PRNR { $$ = std::sin($3); }
| FUNC_COS SYM_PRNL expr SYM_PRNR { $$ = std::cos($3); }
;
%%
void yyerror(char *s)
{
std::cout << ">> %s\n", s;
}
int main()
{
yyparse();
return 0;
}
Copy this to calc.l:
%{
#include <stdlib.h>
#include <stdio.h>
#include "calc.tab.h"
extern YYSTYPE yylval;
void yyerror(char*);
%}
%%
"+" {
printf("T_ADD ");
return OP_ADD;
}
"-" {
printf("T_SUB ");
return OP_SUB;
}
"*" {
printf("T_MUL ");
return OP_MUL;
}
"/" {
printf("T_DIV ");
return OP_DIV;
}
"^" {
printf("T_POW ");
return OP_POW;
}
"=" {
printf("T_EQL ");
return OP_EQL;
}
"(" {
printf("T_PRNL ");
return SYM_PRNL;
}
")" {
printf("T_PRNR ");
return SYM_PRNR;
}
"sin"|"SIN" {
printf("T_SIN ");
return FUNC_SIN;
}
"cos"|"COS" {
printf("T_COS ");
return FUNC_COS;
}
[0-9]+ {
printf("T_INT ");
sscanf(yytext, "%lf", &yylval);
return T_INT;
}
[0-9]+(\.?[0-9]*e?-?[0-9]*)? {
sscanf(yytext, "%lf", &yylval);
printf("T_FLOAT ");
return T_FLOAT;
}
[a-zA-Z]([a-zA-Z]|[0-9])* {
strcpy (yylval.index, yytext);
printf("T_IDEN ");
return T_IDEN;
}
\n {
return EOL;
}
[ \t]+ {}
"quit"|"exit" {
return CMD_EXT;
}
. {
yyerror("ERROR: Unrecognized input!");
}
%%
int yywrap()
{
return 1;
}
Copy this to mem.h:
#ifndef _MEM_H_
#define _MEM_H_
#include <iostream>
#include <map>
#include <string>
std::map<std::string, double> variable_map;
void set_variable(char *index, double val) {
// add variables
variable_map[index] = val;
std::cout << "var " << index << " set\n";
}
double get_variable(char * index) { return variable_map[index]; }
#endif
Create a file named Makefile and copy the following code in it:
.PHONY=all
all: calc run
lex.yy.c: calc.l
flex calc.l
calc.tab.c: calc.y
bison -d calc.y
calc: calc.tab.c lex.yy.c
g++ -o calc calc.tab.c lex.yy.c -lm
run: calc
./calc
Make sure you have already installed flex and bison. If not, you can install them by (using Windows MYSY2):
pacman -S flex bison
Then, run make to compile the code. You will get an executable file named calc. Run it and test it!
It is a calculator that supports basic arithmetic operations, parentheses, and some functions like sin and cos (you can add more functions by your own and create your own syntax!). You can also assign a value to a variable and use it later.
Understanding what has happened#
Just now we wrote a calc.l and a calc.y. In fact, the calc.l is the “lexer description”, and the calc.y is the “parser description”. The lexer is used to split the input into tokens, and the parser is used to parse the tokens and generate the syntax tree. Finally, we used bison and flex to generate the lexer and parser.
What is Lexer and Parser?#
In computer science, lexical analysis, lexing or tokenization is the process of converting a sequence of characters (such as in a computer program or web page) into a sequence of lexical tokens (strings with an assigned and thus identified meaning). [1]

A lexical token or simply token is a string with an assigned and thus identified meaning. It is structured as a pair consisting of a token name and an optional token value. The token name is a category of lexical unit.
Consider this expression in the C programming language:
x = a + b * 2;
The lexical analysis of this expression may yield the following sequence of tokens:
[(identifier, x), (operator, =), (identifier, a), (operator, +), (identifier, b), (operator, *), (literal, 2), (separator, ;)]
We often use regular expression to describe the lexer rules. Regular expression is a sequence of characters that define a search pattern.
Parser is often more complicated than lexer. We have to first define the grammar of the language, and then use the grammar to generate the parser. The parser is used to parse the tokens and generate the syntax tree. Regular expressions are often not good enough to describe the language, so we often use a more powerful tool called context-free grammar to describe the language. Context-free grammar is a formal grammar which describes all possible strings in a given formal language. It is a type of formal grammar, the set of strings which can be generated by the grammar is called the language of the grammar.
Lexical analysis and parsing (syntax analysis) are often the first two steps of compilation.
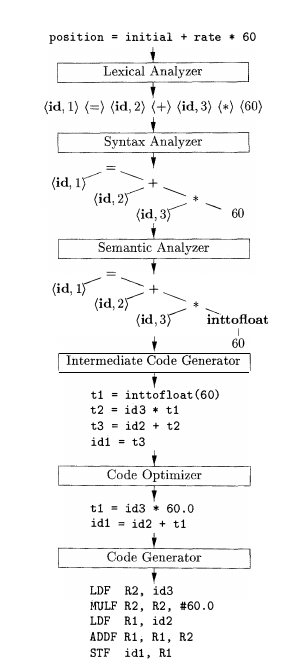
Regular Expression#
Regular expression is used almost everywhere.
Regular expression matcher may have some little difference in different languages (For example, the meaning of ?). You can go to this website to test your regular expression.
Commonly Used Rules#
(python example)
^$.*+?(Two meanings: 1. match 0 or 1 times; 2. match the shortest string)[]()(xx|yy)[a-zA-Z0-9][^a-zA-Z0-9]\s: match any whitespace character\S: match any non-whitespace character
Examples:
Match the following code:
if ( any expression ) { any thing }
Match
http://www.ABC.comandhttps://www.ABC.cnwhereABCcan be anya-zA-Zcharacters.
Context-Free Grammar#
Warning
I don’t have enough time to finish this.